Numeryczne całkowanie równań różniczkowych.
Wstęp.
Jak nietrudno zauważyć, w poruszanych na mojej stronie zagadnieniach przewija się pewien wspólny mianownik. Jest nim numeryczne całkowanie równań różniczkowych (RR), które wykorzystywane jest do symulacji wszelkiej maści obiektów dynamicznych. Temat ten jest bardzo obszerny i warto jest go nieco zgłębić pomimo tego, że wszystkie te metody już dawno zostały przez kogoś zaimplementowane. Z tego miejsca chciałem również mocno polecić książkę Stanisława Osowskiego pt. "Modelowanie i symulacja układów i procesów dynamicznych", która jest przystępnym wyłożeniem obszernej teorii, której urywki przedstawię tutaj.
W ramach tego opracowania omówię 6 metod całkowania równań, których implementacja nie powinna sprawiać problemów nawet początkującym programistom. Będą to metody stałokrokowe, bez zagłębiania się w szczegóły jak chociażby sztywność układów równań. Temat metod niejawnych tylko przytoczę, ponieważich implementacja jest już nieco bardziej skomplikowana i wymaga użycia dodatkowych rozwiązań.
Wszystkie omawiane tutaj metody służą w ogólności do znalezienia przybliżonego rozwiązania układu równań różniczkowych danych w postaci: $$ \frac{d\mb{y}}{dx}=\mb{f}(x,\mb{y}), $$ gdzie: $\mb{y}(x)$ - zmienna wektorowa zależna od $x$, $\mb{f}$ - wektor funkcji liniowych lub nieliniowych. Dany jest również warunek początkowy: $$ \mb{y}(0)=\mb{y}_0. $$ W kontekście układów dynamicznych, w których zmienną jest czas, zaś szukanym rozwiązaniem jest trajektoria $\mb{x}(t)$ równanie to wygodniej jest sformułować jako: $$ \mb{\dot{x}}=\mb{f}(t,\mb{x}), \quad \mb{x}(0)=\mb{x}_0. $$ Warto tutaj zwrócić uwagę na to, że równania różniczkowe są funkcjami tylko stanu i czasu. Jeśli w ich postaci występują inne wielkości niebędące stałymi, konieczne jest zastosowanie odpowiedniej ekstrapolacji. Zazwyczaj używany jest ekstrapolator zerowego rzędu, jednak zadowalającą dokładność rozwiązania można zapewnić tylko wtedy kiedy okres próbkowania jest znacząco mniejszy od szybkości zmian dodatkowych wielkości.
Jako przykład testowy przytoczę tutaj model satelity krążącej wokół masywnego ciała (o czym więcej tutaj: LINK). Przy odpowiednio dobranych warunkach początkowych można łatwo wizualnie ocenić jakość działania algorytmu. Model matematyczny ruchu satelity dany jest w postaci: $$ \frac{d}{dt}\begin{bmatrix}s_x \\ s_y \\ v_x \\ v_y\end{bmatrix} = \begin{bmatrix}v_x \\ v_y \\ -\frac{s_x}{(s^2_x + s^2_y)^{\frac{3}{2}}} \\ -\frac{s_y}{(s^2_x + s^2_y)^{\frac{3}{2}}}\end{bmatrix}, $$ gdzie: $s_x$ i $s_y$ - współrzędne położenia, $v_x$ i $v_y$ - składowe prędkości. Układ celowo został zubożony o masę ciała i stałą grawitacji bo nie mają one tutaj większego znaczenia. Uproszczeniu uległo również wyrażenie na pierwszą prędkość kosmiczną: $$ v=\sqrt{\frac{1}{r}}. $$
Metody z rodziny Rungego-Kutty.
Chyba najpopularniejszą rodziną algorytmów całkowania RR jest grupa metod Rungego-Kutty. Są to metody jednokrokowe, wieloetapowe, tzn. takie, w których do wyznaczenia kolejnych rozwiązań wykorzystywany jest tylko jeden wcześniejszy krok rozwiązania przy czym na jedną iterację algorytmu przypadać może więcej niż jeden etap. Etapy w tym przypadku oznaczają konieczność wielokrotnego wyznaczania wartości równań różniczkowych co wpływa bezpośrednio na wydajność algorytmu. Ideą metod z tej rodziny jest rozwinięcie w szereg Taylora rozwiązania $\mb{x}(t)$ wokół punktu $t_i$: $$ \mb{x}_{i+1}=\mb{x}_i+h\mb{\dot{x}}_i+\frac{1}{2}h^2\mb{\ddot{x}}_i+\dots+\frac{1}{p!}h^p\mb{x}^{(p)}_i+0(h^{p+1}), $$ gdzie: $p$ - rząd rozwinięcia, $\mb{x}^{(p)}$ - p-ta pochodna $\mb{x}$ po czasie, $0(h^{p+1})$ - lokalny błąd odcięcia. Rząd rozwinięcia $p$ odpowiada rzędowi metody. Po uwzględnieniu zależności $\mb{\dot{x}}=\mb{f}(t,\mb{x})$ otrzymuje się: $$ \mb{x}_{i+1}=\mb{x}_i+h\mb{f}(t_i,\mb{x}_i)+\frac{1}{2}h^2\mb{\dot{f}}(t_i,\mb{x}_i)+\dots+\frac{1}{p!}h^p\mb{f}^{(p-1)}(t_i,\mb{x}_i)+0(h^{p+1}). $$ Wyższe pochodne funkcji $\mb{f}$ są w odpowiedni sposób aproksymowane tak, żeby zachować rząd dokładności rozwiązania.
Opis poszczególnych algorytmów zacznę od metody o największej rozpatrywanej przeze mnie ilości etapów. Jest to metoda Rungego-Kutty IV rzędu, która dla każdego kroku rozwiązania wymaga czterokrotnego wyliczenia wartości równań. Jest to metoda często używana ze względu na satysfakcjonującą dokładność i akceptowalny narzut obliczeniowy. Do wyznaczenia kolejnych rozwiązania w chwili $i+1$, konieczne jest wyznaczenie 4 współczynników: $$ \begin{aligned} \mb{k}_1 &=h\mb{f}(t_i,\mb{x}_i) \\ \mb{k}_2 &=h\mb{f}(t_i+0.5h,\mb{x}_i+0.5\mb{k}_1) \\ \mb{k}_3 &=h\mb{f}(t_i+0.5h,\mb{x}_i+0.5\mb{k}_2) \\ \mb{k}_4 &=h\mb{f}(t_i+h,\mb{x}_i+\mb{k}_3) \end{aligned}. $$ Jak widać, konieczne jest wyznaczenie wartości RR nie tylko dla kroku i-tego ale również dla półkroku oraz kroku następnego. Ostatecznie rozwiązanie układu dla chwili następnej dane jest jako: $$ \mb{x}_{i+1} = \mb{x}_i+\frac{1}{6}(\mb{k}_1+2\mb{k}_2+2\mb{k}_3+\mb{k}_4). $$ Metodami mniej złożonymi obliczeniowo są metody rzędu II. Przytoczyć można tutaj dwie najbardziej powszechne, metodę Heuna i punktu pośredniego. Wymagają one wyznaczenia tylko wartości $\mb{k}_1$ i $\mb{k}_2$. Kolejne iteracje dla metody punktu pośredniego dane są: $$ \begin{aligned} \mb{k}_1 &=h\mb{f}(t_i,\mb{x}_i) \\ \mb{k}_2 &=h\mb{f}(t_i+0.5h,\mb{x}_i+0.5\mb{k}_1) \\ \mb{x}_{i+1} &= \mb{x}_i+\mb{k}_2, \end{aligned} $$ zaś dla metody Heuna: $$ \begin{aligned} \mb{k}_1 &=h\mb{f}(t_i,\mb{x}_i) \\ \mb{k}_2 &=h\mb{f}(t_i+h,\mb{x}_i+\mb{k}_1) \\ \mb{x}_{i+1} &= \mb{x}_i+0.5(\mb{k}_1+\mb{k}_2). \end{aligned} $$ Najprostszą z rozpatrywanych metod jest metoda Eulera (algorytm ekstrapolacyjny), gdzie rozwiązanie dane jest w postaci: $$ \mb{x}_{i+1} = \mb{x}_i+\mb{k}_1. $$ Jest to metoda która oferuje najmniejszą dokładność ale też wymaga tylko jednego etapu na krok.
Warto jeszcze wspomnieć, że istnieją metody wyższych rzędów np. Dormanda-Prince'a, zaimplementowana w Matlabie w postaci funkcji ode45. Jest ona nieco bardziej rozbudowana ponieważ oferuje możliwość zmiany kroku całkowania poprzez porównanie IV i V rzędu rozwiązania. Osoby bardziej zainteresowane odsyłam po bardziej ogólne rozważania chociażby tutaj: LINK, gdzie wszystkie metody zaprezentowane są w postaci ogólnych tabel Butchera.
Algorytm Verleta.
Na szczególną uwagę zasługuje algorytm Verleta, który z powodzeniem stosowany jest symulacjach wielu zjawisk fizycznych, w szczególności ruchu ciał. Jest on dosyć unikalny z kilku względów. Dotyczy on problemów rozwiązywania układów RR w postaci: $$ \mb{\ddot{x}}=\mb{a}(t,\mb{x}), $$ gdzie: $\mb{x}$ - wektor współrzędnych będących funkcjami czasu, $\mb{a}$ - wektor przyspieszeń zależnych od wektora $\mb{x}$. Dane są również warunki początkowe: $$ \mb{x}(0)=\mb{x}_0, \quad \mb{v}(0)=\mb{v}_0, $$ gdzie: $\mb{v}$ - prędkości układu, pochodne $\mb{x}$ po czasie. Algorytm Verleta w wersji podstawowej dany jest jako: $$ \mb{x}_{i+1}=2\mb{x}_i-\mb{x}_{i-1}+h^2\mb{a}(t_i,\mb{x}_i). $$ Należy tutaj zwrócić uwagę na dwie istotne kwestie. Algorytm Verleta jest metodą wielokrokową oraz nie uwzględnia on prędkości $\mb{v}_i$. Aby wyznaczyć tą brakującą wielkość należy skorzystać z zależności: $$ \mb{v}_i=\frac{\mb{x}_{i+1}-\mb{x}_{i-1}}{2h}. $$ Aby można było użyć tego algorytmu konieczne jest jej jednokrokowe wystartowanie z użyciem innej metody całkowania. Pozostałym problemem jest jeszcze nieintuicyjne wyznaczanie prędkości. Wariantem powyższego algorytmu jest metoda skokowa (leap-frog method). Modyfikacja ta wykorzystuje półkroki symulacji jednak nie rozwiązuje wszystkich problemów. Najlepszą opcją jest trzeci wariant algorytmu - wersja prędkościowa. Dana jest w postaci: $$ \begin{aligned} \mb{x}_{i+1} &=\mb{x}_i+h\mb{v}_i+0.5h^2\mb{a}_i \\ \mb{v}_{i+1} &=\mb{v}_i+0.5h(\mb{a}(t_i,\mb{x}_i)+\mb{a}(t_{i+1},\mb{x}_{i+1})). \end{aligned} $$ Algorytm ten w jawny sposób wykorzystuje wyznaczanie wartości prędkości dla każdego kroku. Można ten algorytm również zastosować w sytuacji, kiedy równania przyspieszeń zależą od prędkości: $$ \begin{aligned} \mb{x}_{i+1} &=\mb{x}_i+h\mb{v}_i+h^2\mb{a}(t_i,\mb{x}_i) \\ \mb{v}_{i+1} &=\mb{v}_i+h\mb{a}(t_{i},\mb{x}_{i}), \end{aligned} $$ jednak odbywa się to kosztem dokładności. Niewątpliwą zaletą tego algorytmu jest prostota oraz mała złożoność obliczeniowa. Z kolei do wad zaliczyć trzeba dosyć ograniczoną klasę problemów, w której znajduje ona zastosowanie.
Algorytm Adamsa-Bashfortha.
Osobną grupę algorytmów stanowią metody wielokrokowe w tym najprostszy z nich - Algorytm Adamsa-Bashfortha. Do wyznaczenia rozwiązania układu RR konieczna jest znajomość $p$ wcześniejszych rozwiązań. Metody wielokrokowe, w przeciwieństwie do metod jednokrokowych, do przybliżenia postaci rozwiązania wykorzystują funkcję wielomianową. Aproksymacja wielomianem rzędu $p$ oznacza zastosowanie metody rzędu p-tego.
Ogólna postać rozwiązania dana jest według zależności: $$ \mb{x}_{i+1}=\mb{x}_i+h\sum^{p-1}_{j=0}b_i\mb{f}(t_{i-j},\mb{x}_{i-j}), $$ gdzie: $b_i$ do odpowiednio dobrane współczynniki. Dla użytej w teście metody IV rzędu, rozwiązanie dane jest bezpośrednio jako: $$ \mb{x}_{i+1}=\mb{x}_i+\frac{h}{24}(55\mb{f}(t_{i},\mb{x}_{i})-59\mb{f}(t_{i-1},\mb{x}_{i-1})+37\mb{f}(t_{i-2},\mb{x}_{i-2})-9\mb{f}(t_{i-3},\mb{x}_{i-3})). $$ Zasadniczą wadą metody jest to, że algorytm rzędu $p$ wymaga znajomości $p$ startowych wartości funkcji $\mb{f}$. Należy więc "wystartować" algorytm z użyciem innej metody całkowania. Zaletą zaś jest to, że dla każdego kroku wymaga tylko jednego wyznaczania wartości $\mb{f}$.
Algorytmy predyktor-korektor.
Powyżej omówione zostały metody, których rozwiązania dane są w postaci jawnej, takiej, że do wyznaczenia rozwiązania w chwili obecnej, potrzebne są wielkości wyznaczane w chwilach poprzednich. Wspomniałem we wstępie, że istnieją też metody niejawne jak np. algorytm interpolacyjny Eulera: $$ \mb{x}_{i+1}=\mb{x}_{i}+h\mb{f}(t_{i+1},\mb{x}_{i+1}). $$ Wielkość $\mb{x}_{i+1}$ występuje tutaj po obu stronach równania. Aby sobie poradzić z tym problemem najprościej jest rozbudować metody niejawne do postaci predyktor-korektor. Ideą tego postępowania jest estymacja obecnej wartości $\mb{x}_{i+1}$, która z kolei ląduje w równaniu korektora, czyli metody niejawnej.
Jako przykład niech posłuży ostatni z omawianych algorytmów czyli Adams-Bashforth (AB). W skrypcie przygotowanym na potrzeby tego opracowania umieściłem również implementację metody Adamsa-Moultona (AM), która wykorzystuje predykcję z użyciem metody AB. Równania takiej kombinacji dane są w postaci: $$ \mb{\tilde{x}}_{i+1}=\mb{x}_i+\frac{h}{24}(55\mb{f}(t_{i},\mb{x}_{i})-59\mb{f}(t_{i-1},\mb{x}_{i-1})+37\mb{f}(t_{i-2},\mb{x}_{i-2})-9\mb{f}(t_{i-3},\mb{x}_{i-3})), $$ co stanowi etap predykcji, zaś ocena $\mb{\tilde{x}}$ ląduje następnie w docelowym równaniu metody AM: $$ \mb{x}_{i+1}=\mb{x}_i+\frac{h}{24}(9\mb{f}(t_{i+1},\mb{\tilde{x}}_{i+1})-19\mb{f}(t_{i},\mb{x}_{i})-5\mb{f}(t_{i-1},\mb{x}_{i-1})+\mb{f}(t_{i-2},\mb{x}_{i-2})). $$ Metoda daje zdecydowanie bardziej dokładne wyniki jednak wymaga dodatkowego nakładu obliczeniowego. Powyższe rozumowanie zastosować można również dla innych metod niejawnych.
Implementacja.
Na potrzeby tego opracowania stworzono skrypty Matlaba, które implementują wspomniany wyżej model dynamiczny ruchu satelity i wszystkie metody całkowania RR. Całość zorganizowana jest w 3 plikach:
- test.m - skrypt uruchamiający implementujący wszystkie metody całkowania,
- testMdl.m - funkcja implementująca model matematyczny satelity,
- plotCircle.m - funkcja malująca okrąg.
Wyniki uruchomienia skryptu przedstawiono poniżej:
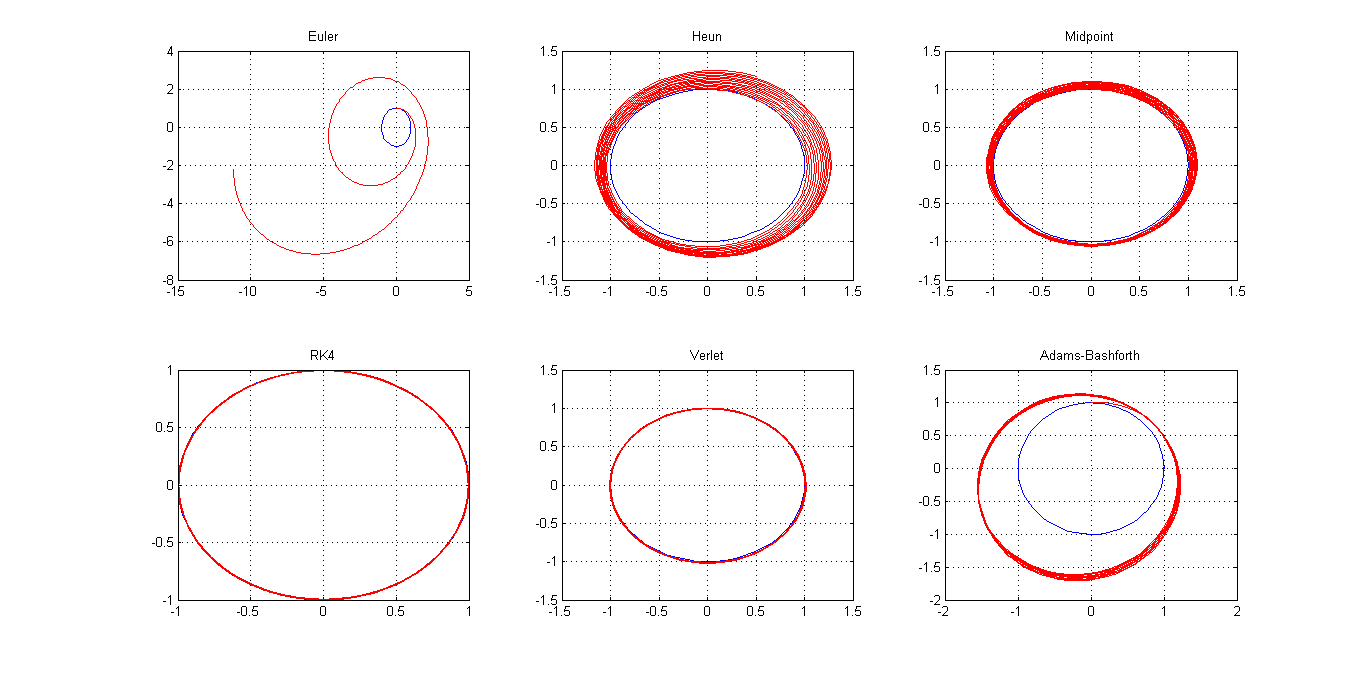
Powyższe wykresy wymagają dodatkowego komentarza. Jak nietrudno się domyślić, metoda Eulera jest niestabilna i już po kilku iteracjach, trajektoria ucieka daleko od referencji. Metody drugiego rzędu są już znacząco lepsze jednak metoda punktu pośredniego okazuje się oferować lepsze wyniki niż algorytm Heuna. Jak można było się spodziewać, metoda RK4 jest stabilna i nawet dla dużego okresu próbkowania oferuje satysfakcjonujące wyniki. Algorytm Verleta również jest stabilny i oferuje wystarczającą dokładność rozwiązania. Metoda Adamsa-Bashfortha poskutkowała niewłaściwym rozwiązaniem, jest jednak jedno ale. Dużo zależy od dokładności metody startującej algorytm. Przykład powyżej pokazuje 4 pierwsze kroki z użyciem Eulera. Przy użyciu RK4 wyniki są znacząco lepsze co polecam sprawdzić. Warto jeszcze zwrócić uwagę na wydajność algorytmów. Dla zadanego problemu, najefektywniejszym rozwiązaniem jest algorytm Verleta, a jeśli można pozwolić sobie nieco mniejszą wydajność, warto rozważyć użycie metody RK4.

