Odwrócone wahadło

Wstęp.

Jednym z moich niespełnionych automatycznych snów jest budowa odwróconego wahadła. Niestety póki co na tego typu przedsięwzięcie brak mi zasobów czasowych co nie oznacza, że pomysł należy całkowicie zarzucić. Można, a nawet wypadałoby zacząć projekt budowy wahadła od zapoznania się z minimum teorii, które jest z nim nierozerwalnie powiązane. Tutaj na ratunek przychodzą wszelkiej maści środowiska symulacyjne oraz modelowanie. Tematem niniejszego opracowania będzie zatem symulacja i synteza układów sterowania dla odwróconego wahadła.

Czemu wybór padł akurat na wahadło? Największą jego zaletą jest szerokie spektrum zagadnień z zakresu automatyki i sterowania, z którymi należy się zapoznać, aby tchnąć nieco życia w tego typu obiekt. Odwrócone wahadło prezentuje wysoką wartość dydaktyczną dlatego w Internecie można znaleźć wiele filmów i materiałów (w większości przypadków stworzonych w ramach działalności akademickiej) prezentujących działanie kompletnego układu sterowania wahadłem w praktyce.

Informacje ogólne.

Zasadniczo odwrócone wahadło nie różni się od swojego "zwykłego" odpowiednika. Jest to swobodnie wiszący pręt przymocowany do wózka. Wózek z kolei ma możliwość poruszania się w jednym wymiarze (oczywiście nic nie stoi na przeszkodzie, żeby próbować rozszerzyć problem wahadła do dwóch wymiarów). Napęd wózka zazwyczaj zrealizowany jest z użyciem przekładni pasowej (choć można znaleźć też inne ciekawe sposoby realizacji stanowisk). Taki układ jest ciekawy z dwóch zasadniczych powodów:

posiada dwa punkty równowagi: stabilny, kiedy wahadło spoczywa w położeniu dolnym i niestabilny, kiedy wahadło skierowane jest pionowo ku górze,
odwrócone wahadło jest obiektem niedosterowanym ponieważ wielkości sterowanych możemy wyróżnić więcej niż jest wejść w układzie.

Jedyną wielkością, którą można wpływać na stan układu jest siła przyłożona do wózka, którego przemieszczanie się wprawia w ruch wahadło. Można wyróżnić tutaj kilka celów dla układu regulacji. Najważniejszym z nich jest stabilizacja wahadła w położeniu górnym. Drugim jest regulacja położenia wózka w odniesieniu do całego stanowiska. Trzecim, niemniej ważnym, jest realizacja algorytmów umożliwiających rozbujanie wahadła z pozycji dolnej i doprowadzenie go to pozycji górnej. Całość dopełniają jeszcze zagadnienia związane z pomiarami wielkości charakteryzujących ruch wahadła, filtracją i estymacją.

Nic tak do wyobraźni nie przemawia jak obraz, szczególnie ruchomy dlatego, żeby zaprezentować to o czym mowa w pełnej krasie, posłużę się filmem autorstwa dwóch Polaków, pana Kamila Troca i pana Marcina Wiśniewskiego:

Film jest jeszcze świeży i przedstawia praktyczną realizację regulacji PID w stabilizacji odwróconego wahadła. Na dokładkę dorzucę jeszcze jeden film, tym razem z wahadłem podwójnym w roli głównej. Moim zdaniem, działanie układu robi rewelacyjne wrażenie:

Odwrócone wahadło - modele matematyczne.

Po małym zanużeniu się w Internecie w poszukiwaniu modelu matematycznego odwróconego wahadła udało mi się znaleźć mnóstwo prac traktujących o tym zagadnieniu. Najlepiej przyswajalne wyprowadzenie modelu można znaleźć tutaj: LINK. Autorzy wyprowadzili model krok po kroku i z całego serca polecam zapoznać się z tym opracowaniem. Jedyną rzeczą, której moim zdaniem brakuje jest doprowadzenie postaci równań różniczkowych modelu pełnego do formy, która byłaby bezproblemowa w implementacji np. w Simulinku.

Zgodnie ze wspomnianym dokumentem, model matematyczny odwróconego wahadła dany jest w postaci: $$ \begin{equation} \left(M + m\right)\ddot{x}+b\dot{x}=F+mL\dot{\theta}^2\sin{\theta}-mL\ddot{\theta}\cos{\theta} \label{mdl1} \end{equation} $$ $$ \begin{equation} \left(I+mL^2\right)\ddot{\theta}=mgL\sin{\theta}-mL\ddot{x}\cos{\theta} \label{mdl2} \end{equation}, $$ gdzie: $x$ - położenie wózka w $[m]$, $\theta$ - kąt odchylenia wahadła w $[rad]$. Warto zwrócić uwagę, że kąt $\theta$ jest miarą odchylenia wahadła od pionu, a wzrost jego wartości odbywa się w kierunku zgodnym z ruchem wskazówek zegara. Wielkość $F$ jest siłą przyłożoną do wózka, która wprawia go w ruch. Pozostałe parametry występujące w powyższym równaniu to:

Wielkość	Wartość i jednostka
$M$ - masa wózka	$0.5 kg$
$m$ - masa wahadła	$0.2 kg$
$L$ - połowa długości wahadła	$0.3 m$
$I$ - moment bezwładności wahadła	$0.006 kgm^2$
$b$ - współczynnik tarcia wózka	$0.1 \frac{N}{ms^{-1}}$
$g$ - przyspieszenie ziemskie	$9.80665 \frac{m}{s^2}$

Swoją drogą, powyższe parametry widziałem przynajmniej w 3 miejscach w trakcie poszukiwań modelu wahadła. Oczywiście taki model nie nadaje się do implementacji bezpośrednio np. w Simulinku. Konieczne jest wyrugowanie z równań pochodnych $\ddot{\theta}$ oraz $\ddot{x}$. Wyznaczając te wielkości z równania $\ref{mdl2}$ i wstawiając je do równania $\ref{mdl1}$ otrzymuje się model: $$ \begin{equation} \ddot{\theta}=\frac{1}{q}\left(FmL\cos{\theta}-bmL\dot{x}\cos{\theta}-\left( M+m\right)mLg\sin{\theta}+m^2L^2\dot{\theta}^2\sin{\theta}\cos{\theta} \right) \end{equation} $$ $$ \begin{equation} \ddot{x}=\frac{1}{q}\left[\left(I+mL^2\right)\left(-F+b\dot{x}-mL\dot{\theta}^2\sin{\theta}\right)+m^2L^2g\sin{\theta}\cos{\theta}\right], \end{equation} $$ gdzie: $q=m^2L^2\cos^2{\theta}-\left(M+m\right)\left(I+mL^2\right)$. Taki model można już śmiało implementować w Simulinku bez obawy o pętle algebraiczne. Z racji tego, że powyższy model jest modelem nieliniowym, zaś sama regulacja będzie odbywała się w okolicach punktu pracy $\theta_{0}=0$, należy pokusić o linearyzację powyższych równań wokół niego przymując poniższe założenia: $$ \begin{equation} \sin{\theta}\approx\theta, \quad \cos{\theta}\approx 1, \quad \dot{\theta}^2\approx 0, \quad I=0 \end{equation} $$ Założenia te doprowadzają model matematyczny do liniowej postaci: $$ \begin{equation} \ddot{\theta}=\frac{\left(M+m\right)g}{ML}\theta+\frac{b}{ML}\dot{x}-\frac{F}{ML} \end{equation} $$ $$ \begin{equation} \ddot{x}=-\frac{mg}{M}\theta-\frac{b}{M}\dot{x}+\frac{F}{M}. \end{equation} $$ Wprowadzając wektor stanu w postaci: $$ \begin{equation} \mb{x}= \begin{bmatrix} \dot{\theta} & \theta & \dot{x} & x \end{bmatrix}^T, \end{equation} $$ otrzymuje się model nieliniowy wahadła: $$ \begin{equation} \dot{\mb{x}}=f\left(\mb{x},F\right), \end{equation} $$ oraz model liniowy, sprowadzony do postaci równań stanu: $$ \begin{equation} \dot{\mb{x}}=\mb{Ax}+\mb{B}u, \end{equation} $$ gdzie: $u$ - siła $F$ przyłożona do wózka. Macierze $A$ i $B$ równe są: $$ \begin{equation} \mb{A}= \begin{bmatrix} 0 & \frac{\left(M+m\right)g}{ML} & \frac{b}{ML} & 0 \\ 1 & 0 & 0 & 0 \\ 0 & -\frac{mg}{M} & -\frac{b}{M} & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}, \quad \mb{B}= \begin{bmatrix} -\frac{1}{ML} \\ 0 \\ \frac{1}{M} \\ 0 \end{bmatrix}. \end{equation} $$ Można byłoby pokusić się jeszcze o dodatkowe wyprowadzenie interesujących nas transmitancji układu (oczywiście dla układu liniowego): $$ \begin{equation} K_1(s)=\frac{\theta(s)}{U(s)}, \quad K_2(s)=\frac{X(s)}{U(s)}, \end{equation} $$ jednak nie będą one szczególnie przydatne, a samo ich wyznaczenie można zrealizować z użyciem dostępnych w Matlabie komend (w Octave konieczna jest dodatkowa instalacja pakietu Control: LINK).

Problem stabilizacji - regulacja PID.

Na pierwszy ogień w starciu z odwróconym wahadłem idzie regulator PID. Na jego temat napisano już wiele także ja ograniczę się do absolutnego minimum, a po więcej informacji odsyłam do fachowej literatury bo wbrew pozorom jest to bardzo szerokie zagadnienie. PID jest chyba najczęściej stosowanym regulatorem, zarówno w zastosowaniach amatorskich jak i profesjonalnych. Swój sukces zawdzięcza przede wszystkim swojej prostocie i uniwersalności. Składa się z 3 członów: proporcjonalnego $P$, który reaguje na obecne wartości uchybu (uchyb jest sygnałem będącym różnicą pomiędzy wartością zadaną, a wartością mierzoną wielkości regulowanej), $I$, czyli członu całkującego, który przechowuje w sobie informacje o przeszłych wartościa uchybu oraz $D$, człon różniczkujący, który reaguje na przyszłe wartości uchybu. Równanie czasowe szeregowego, idealnego regulatora PID przedstawia się następująco: $$ \begin{equation} u(t) = K_p \left(e(t)+\frac{1}{T_i}\int_{0}^{t}{e(\tau)}d\tau + T_d\frac{de(t)}{dt} \right), \end{equation} $$ gdzie: $u(t)$ - sygnał sterujący z regulatora, $e(t)$ - uchyb regulacji, $K_p$, $T_i$, $T_d$ - parametry poszczególnych członów i nastawy regulatora. Jest to klasyczne równanie pozycyjnego algorytmu PID. W dziedzinie operatorowej równanie przedstawia się następująco: $$ \begin{equation} G(s)=\frac{U(s)}{E(s)}=K_p \left(1+\frac{1}{sT_i}+sT_d\right), \end{equation} $$ zaś najczęściej spotykana postać regulatora PID w postaci dyskretnej, którą wykorzystałem już wcześniej w LINK przedstawia się: $$ \begin{equation} u(i)=K_p\left(e(i)+\frac{h}{T_i}\sum_{k=0}^{i} e(k)+T_d\frac{e(i)-e(i-1)}{h}\right). \end{equation} $$ W większości przypadków, praktyczna implementacja regulatora PID obejmuje również takie mechanizmy jak:

mechanizm anti-windup,
ograniczenie wartości sterującej lub jej przyrostu,
przełączanie bezuderzeniowe,
modyfikacje członu różniczkującego.

Jak zostało wspomniane wcześniej, układ odwrotnego wahadła jest przykładem systemu, który jest niedosterowany. Jeśli podstawą działania układu regulacji ma być tylko zerowanie kąta odchylenia wahadła $\theta$, wtedy nie ma większego problemu poniewać dysponujemy jedną wielkością regulowaną i jednym sterowaniem. Problem pojawia się w sytuacji kiedy chcemy, aby układ dodatkowo stabilizował położenie samego wahadła. Wielkości regulowane są dwie przy braku dodatkowych wielkości regulujących. Rozwiązaniem tego zagadnienia jest rozbudowa struktury układu sterowania i wydzielenie dwóch osobnych regulatorów dla każdej wielkości regulowanej z osobna. W literaturze można spotkać się z dwoma podejściami:

układ regulacji kaskadowej
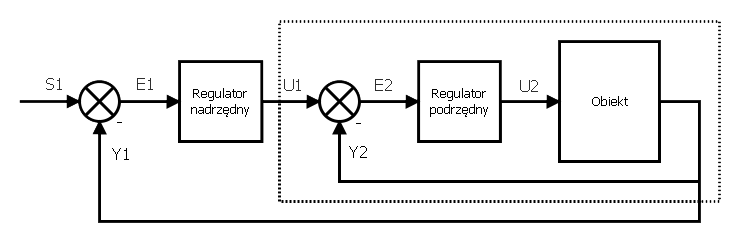
układ regulacji dwóch równoległych regulatorów.

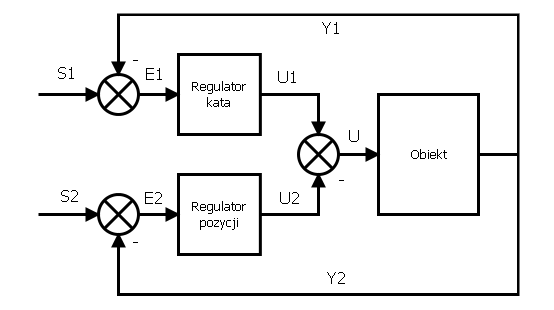
Na powyższych schematach oznaczono poszczególne sygnały jako: $S$ - wartości zadane, $U$ - sterowania z regulatorów, $E$ - uchyby regulacji, $Y$ - wyjścia obiektów. Pierwsze podejście, bardziej klasyczne prezentuje działanie pętli wewnętrznej i zewnętrznej. Zadaniem regulatora nadrzędnego jest wypracowanie wartości zadanej dla wewnętrznego układu regulacji. Dodatkowo należy nadmienić, że aby powyższa idea sterowania miała sens, pętla wewnętrzna musi być dużo "szybsza" od zewnętrznej. Strojenie tego typu struktur zacząć należy od odpowiedniego dobrania parametrów regulatora podrzędnego. W przypadku wahadła, regulacja wewnętrzna zajmuje się stabilizacją kąta $\theta$, zaś pętla zewnętrzna steruje położeniem wózka.

Drugi sposób sterowania działa podobnie z tym, że sterowanie podawane na układ jest różnicą dwóch sterowań. Aby taki układ miał szanse działać prawidłowo należy zadbać o to, aby sterownik odchylenia wahadła był dużo szybszy niż regulator położenia. Regulator położenia traktuje wtedy dodatkowe sterowania jako zakłócenie wejścia układu. W przypadku agresywnych nastaw oby regulatorów, będą one wzajemnie się zakłócać powodując nieprawidłowe działanie całego układu.

Warto zwrócić uwagę na to, że regulator stabilizujący wahadło w pozycji pionowej musi zawierać człon całkujący aby możliwe było zerowanie uchybu w stanie ustalonym. Sytuacja ma się nieco inaczej w przypadku stabilizacji pozycji wózka. Jeśli potraktujemy to jako układ poruszającego się ciała o masie: $M^*=M+m$, gdzie ruch wahadła będzie traktowany jako zakłócenie, a sam wózek stawia pewien dynamiczny opór, uzyskamy równanie różniczkowe: $$ M^*\ddot{x}=F-b\dot{x}. $$ Dokonując obustronnej transformaty Laplace'a i wyznaczając transmitancję: $$ K(s)=\frac{X(s)}{F(s)}=\frac{1}{M^*s^2+bs}, $$ widzimy, że układ ma charakter całkujący (człon $\frac{1}{s}$ można wyciągnąć przed całość). Jest to układ astatyczny pierwszego rzędu stąd wystarczający do celu stabilizacji powinien być regulator PD. Dodatkowy człon całkujący w torze sterowania pogorszy tylko właściwości dynamiczne układu.

Rzeczą na którą również należy zwrócić uwagę, a która może pochłonąć sporo czasu spędzonego nad symulacjami jest to, że omawiany w ramach tego opracowania model wymaga dodatniego, a nie ujemnego sprzężenia w torze stabilizacji położenia wahadła. Związane jest to z tym, że dodatnia wartość sterowania (siły przyłożonego do wózka), powoduje spadek wartości kąta odchylenia. Aby nie zaciemniać obrazu, przeciwny znak regulacji uwzględniony jest we wzmocnieniu regulatora. Jest to podobna sytuacja co w przypadku regulacji poziomu cieczy w zbiorniku z użyciem zaworu wylotowego (i stałego dopływu czynnika). Jeśli wzrost wartości sterowania powoduje mocniejsze otworzenie się zaworu i ubytek cieczy, wtedy również konieczna jest zmiana znaku regulatora. Doskonale widać to w przypadku dokonywania identyfikacji takiego układu z użyciem skoków jednostkowych sterowania (poziomu otwarcia zaworu). Wzrost poziomu otwarcia zmniejsza poziom cieczy co daje ujemne wzmocnienie układu, stąd przy przeliczeniach uzyskuje się "ujemne" nastawy regulatora PID.

Z użyciem linii pierwiastkowych przeprowadzono strojenie regulatora PID stabilizującego samo wahadło. Uzyskane w ten sposób nastawy przyjęły następujące wartości: $$ K_p=-50.8, \quad T_i=7.26, \quad T_d=0.24, $$ dla struktury szeregowej regulatora. Nastawy regulatorów pozycji wózka uzyskano w sposób eksperymentalny. Nastawy regulatorów pozycji oraz efekt działania ostatecznych struktur regulacji (czas symulacji $5s$, warunek początkowy $\theta_0=\frac{\pi}{10})$ przedstawiono w tabeli poniżej:

Str. kaskadowa	Str. równoległa
$K_p=0.05, T_i=\infty, T_d=0.7$	$K_p=6, T_i=\infty, T_d=1.5$

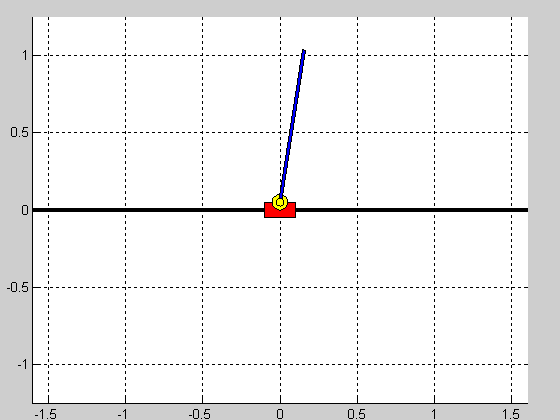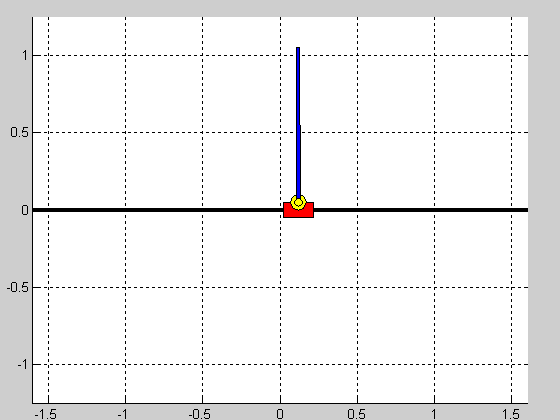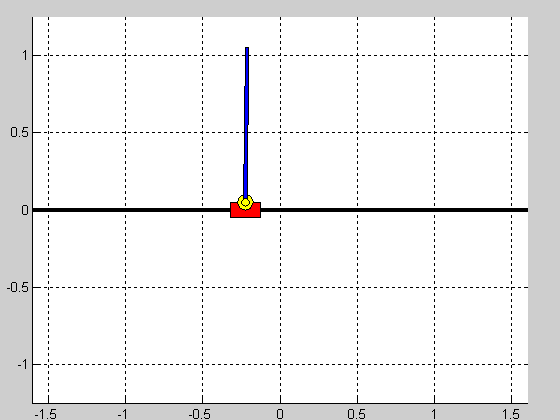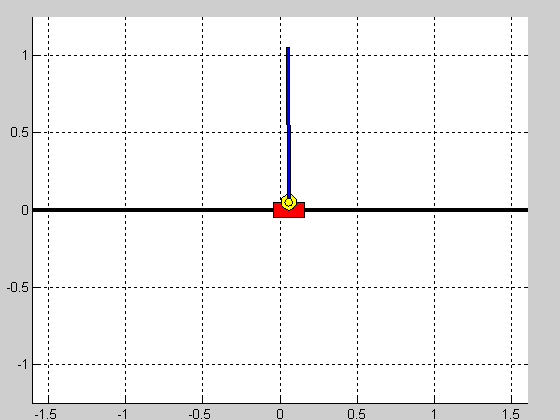
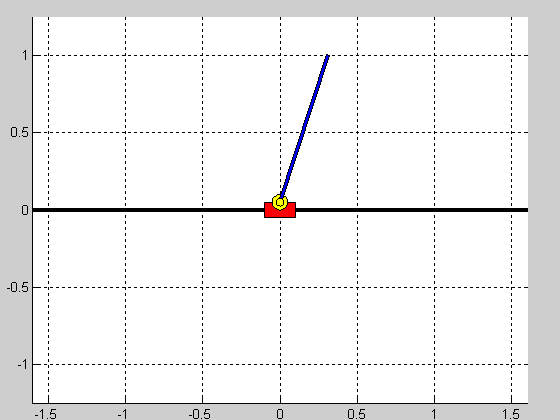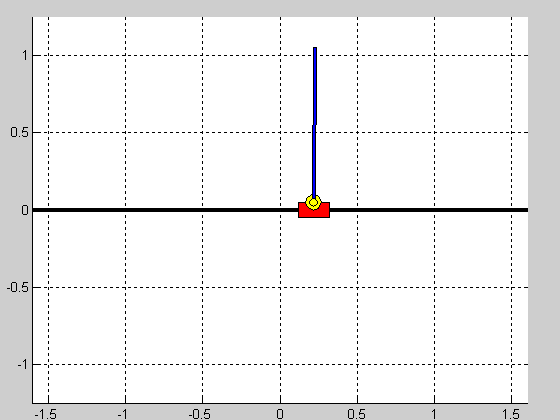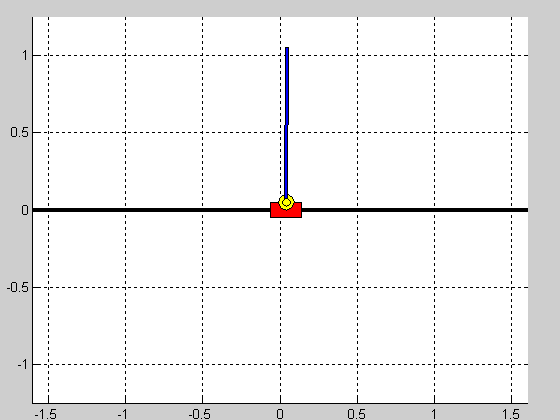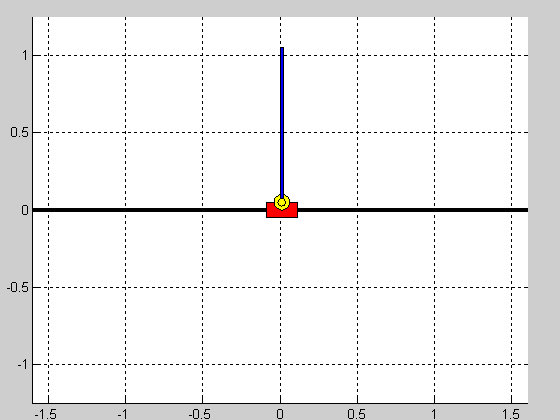
Struktura równoległa działa prawidłowo i jej nastrojenie nie sprawiało większych problemów. Niestety struktura kaskadowa okazała się być wyzwaniem i jej nastrojenie to dosyć karkołomne zadanie. Wydaje się więc, że taka forma sterowania wahadłem jest niewłaściwa.

Problem stabilizacji - LQR.

Drugim, często spotykanym sposobem realizacji sterowania wahadłem w problemie jego stabilizacji jest wykorzystanie regulatora liniowo-kwadratowego (Linear-Quadratic Regulator). Choć początkowo może się ten sposób wydawać kosmiczny, w praktyce jest dosyć łatwy do implementacji, a narzędzia dostarczone z Matlabem w zasadzie w całości rozwiązują problem wszelkich obliczeń, które LQR ze sobą niesie. LQR jest regulatorem bazującym na zasadach sterowania optymalnego w zastosowaniu do układów liniowych, a jego celem jest minimalizacja kwadratowego wskaźnika jakości (funkcji kosztów) danego jako: $$ \begin{equation} J=\int_{0}^{\infty}\left(\mb{x}^T \mb{Q} \mb{x} + \mb{u}^T \mb{R} \mb{u}\right)dt, \end{equation} $$ gdzie $\mb{x}$ oraz $u$ są ciągłymi funkcjami czasu. Funkcję kosztów można intepretować jako karę nałożoną na wartości stanu układu oraz sterowania. Macierz $\mb{Q}$ i $\mb{R}$ są tutaj wagami mówiącymi o tym jaki duży ciężar kary związany jest z poszczególnymi składowymi stanu i sterowania. Są to zatem parametry strojące regulator LQR i to od nich zależą ostatecznie właściwości układu regulacji. Należy też pamiętać o wymiarowości macierzy. Jeśli stan jest wektorem o ilości elementów $m$, a sterowanie zawiera $n$ składowych to macierze $\mb{Q}$ i $\mb{R}$ są macierzami diagonalnymi o nieujemnych wartościach na głównych przekątnych i rozmiarach kolejno $m\times m$ i $n\times n$.

Rozwiązaniem problemu liniowo-kwadratowego dla problemu regulacji jest wektor wzmocnień $\mb{K}$, do wyznaczenia której konieczne jest rozwiązanie równania Riccatiego. Aby dla danego problemu zawsze istniało rozwiązanie należy zapewnych sterowalność regulowanego obiektu. Sterowalność mówi o tym, że istnieje możliwość przeprowadzenia układu z dowolnego warunku początkowego do zadanego warunku końcowego w skończonym czasie. Aby sprawdzić czy dany układ jest sterowalny należy spawdzić rząd macierzy sterowalności danej w postaci: $$ \begin{equation} \mb{S}=\begin{bmatrix}\mb{B} & \mb{AB} & \mb{A}^2\mb{B} & \ldots & \mb{A}^{n-1}\mb{B} \end{bmatrix}, \end{equation} $$ gdzie: $n$ - rząd układu. Jeśli rząd tej macierzy $\mb{S}$ jest równy rzędowi układu, wtedy układ jest sterowalny. Do sprawdzenia sterowalności można użyc funkcji dostarczonej przez Matlaba ctrb(A,B), której parametrami są macierze $\mb{A}$ i $\mb{B}$.

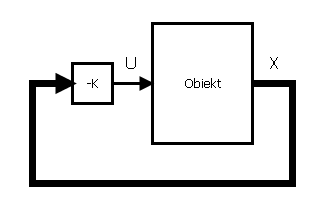
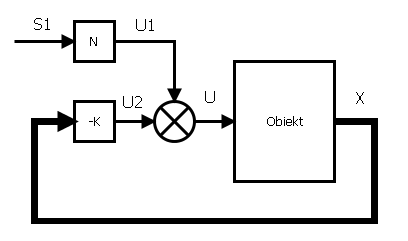
Sterowanie w torze zamkniętym dla regulatora LQR dane jest w postaci: $$ \begin{equation} \mb{u}=-\mb{Kx}, \end{equation} $$ gdzie: $\mb{K}$ - macierz wzmocnień. Pętle regulacji dla układów bez wartości zadanej oraz z nią przedstawiono na rysunkach poniżej:

Struktura sterowania w przypadku regulacji LQR jest znacząco prostsza i zawiera w sobie tylko sprzężenie od stanu układu (w tym przypadku wyjściem układu jest jego stan, w przeciwnym razie konieczne byłoby zastosowanie obserwatora stanu lub dodatkowe przekształcenia). Pierwsze podejście prezentuje zerowe wartości zadane. Jeśli istnieje potrzeba dodania niezerowych wartości zadanych konieczne jest dodanie odpowiedniego sygnału przemnożonego przez $N$ do sygnału regulatora LQ co widać na prawym schemacie. Wartość $N$ można przyjąć jako odpowiadająca danemu sygnałowi wartość z wektora wzmocnień $K$.

Jak zostało wspomniane, strojenie regulatora LQR polega na odpowiednim doborze macierzy $\mb{Q}$ i $\mb{R}$. Należy tutaj zwrócić uwagę na stosunek poszczególnych wartości tych macierzy, a nie ich wartość bezwzględną. W zależności od stawianych układowi regulacji wymagań oraz rzeczywistych, konstrukcyjnych ograniczeń układu sterowania można dopasować wartości $\mb{Q}$ i $\mb{R}$ tak, aby uzyskać zadowalające efekty regulacji. Często jednak proces strojenia sprowadza się do żmudnego testowania wielu konfiguracji w poszukiwaniu satysfakcjonujących nastaw.

Aby lepiej zaprezentować ideę strojenia regulatora LQR warto wypunktować kilka przykładowych scenariuszy.

Jeśli chcemy, aby układ reagował mniej agresywnie, przy użyciu mniejszych wartości sterowań (np. gdy dana jest pewna aprioryczna wiedza mówiąca, że wielkości sterujące są "kosztowne" lub istnieją pewne konstrukcyjne ograniczenia w procesie) wtedy wartości macierzy $\mb{R}$ powinny być znacząco większe niż macierzy $\mb{Q}$. Oznacza to, że wartość wskaźnika jakości będzie gwałtownie rosła jeśli regulator zastosuje większe wartości sterowania. Skutkuje to wolniejszą odpowiedzią układu. Scenariusz odwrotny, kiedy wartości $\mb{R}$ są niskie w stosunku do $\mb{Q}$ skutkuje mniejszą karą za sterowania i w rezultacie powinno to skutkować szybszymi odpowiedziami układu.
Jeśli zakładamy, że regulator ma pilnować wartości pewnych składowych wektora stanu, tak aby ich wartości nie przekraczały pewnych granic, należy odpowiednio dobrać wartości macierzy $\mb{Q}$. Jeśli element $q_i$ macierzy $\mb{Q}$ będzie znacząco większy od $q_j$, wtedy regulator będzie skuteczniej minimalizował element stanu $x_i$ ograniczając jego wartość, "uwalniając" element $x_j$.
Jeśli któryś ze współczynników macierzy $\mb{Q}$ lub $\mb{R}$ przyjmiemy równy 0, oznacza to, że w procesie minimalizacji nie występuje kara za wartość odpowiadającego mu elementu wektora stanu lub sterowania.

Przykładowy, prosty skrypt Matlaba realizujący strojenie regulatora LQR dla problemu odwróconego wahadła przedstawiono poniżej. Z racji, iż istnieje tylko jeden sygnał sterujący, macierz $\mb{R}$ upraszcza się do wielkości skalarnej. Założono również, że na prędkości w układzie nie nakłada się żadnej kary. Wykorzystano tutaj zlinearyzowany model wahadła wyprowadzony we wcześniejszych równaniach.

Plik: strojenie_lqr.m

clearvars;

M = 0.5; % masa wozka
m = 0.2; % masa wahadla
L = 0.3; % dlugosc od mocowania do srodka ciezkosci wahadla
b = 0.1; % wspolczynnik tarcia wozka
g = 9.80665; % przyspieszenie ziemskie

A = [0, g * (M + m) / (M * L), b / (M * L), 0;
    1, 0, 0, 0;
    0, -g * m / M, -b / M, 0;
    0, 0, 1, 0];
B = [-1/(M * L);
    0;
    1/M;
    0];
C = [1 1 1 1];
D = 0;

% test obserwowalnosci
ob = obsv(A,C);
rank(ob)
% test sterowalnosci
ct = ctrb(A,B);
rank(ct)

% lqr
Q = diag([0 1000 0 100]);
R = 1;
K = lqr(A,B,Q,R);
disp(['K = [',num2str(K(1)),',',num2str(K(2)),',',num2str(K(3)),',',num2str(K(4)),'];']);

Po uruchomieniu powyższego skryptu otrzymać można nastawy regulatora LQ: $$ K=\begin{bmatrix}-6.6845 & -51.6047 & -9.6527 & -10\end{bmatrix}, $$ dla których 5 sekund symulacji wahadła (model pełny, nieliniowy) z warunkiem początkowym $\theta_0=\frac{\pi}{10}$ daje nastepujące wyniki: odwrócone wahadło

Implementacja w środowisku Simulink.

Powyższe rozważania zostały przeniesione do środowiska symulacyjnego Simulink. Zaimplementowano pełny model wahadła oraz jego zlinearyzowaną postać w formie S-funkcji (bardzo przydatne narzędzie, którego krótki i treściwy opis można znaleźć tutaj: LINK) oraz utworzono omówione struktury regulacji. Paczka całego projektu zawiera elementy wymienione poniżej.

launcher_simulink.m - skrypt uruchamiający symulację, zawierający w sobie wszystkie niezbędne wielkości i parametry.
stabilizacja_pid_kaskada.slx - implementacja kaskadowego układu regulacji.
stabilizacja_pid_rownolegle.slx - implementacja układu dwóch równoległych PIDów.
stabilizacja_lqr.slx- implementacja regulacji LQR.
plots.m - skrypt wyświetlający uzyskane wyniki symulacji.
anims.m - skrypt uruchamiający prostą animację ruchu wahadła. Skrypt wykorzystuje podejście obiektowe w programowaniu, obiekt patch jako składowe wózka oraz obiekt timer do odmierzania czasu i rysowania "real-time".
timerFcn.m - funkcja timera która rysuje animację i dodatkowo może tworzyć gif z uzyskanych ramek.

Wersję projektu z dnia 18.10.2015 r. można pobrać stąd: LINK.

[Edit 2017/06/11]

Na GitHubie udostępniam wszystkie skrypty jakie zgromadziłem w trakcie przygotowywania tego opracowania. W folderze pdfs można znaleźć przypadne publikacje, które mogą okazać się przydatne w trakcie zagłębiania się w zagadnienie: Inverted-Pendulum.

[TODO]

problem rozbujania wahadła
synteza regulatorów w jeden kontroler